| Complexity level: | 8 |
| Project cost ($): | 20 |
| Time required: | 1 hour to prepare, 1 day for research |
| Material availability: | Easily found |
| Safety concerns: | Handle the paper cutter with care to avoid injury Adult assistance is required. |
Hypothesis
Overview
Scientific Terms
Materials
Procedure
1. A hexagon template is made using a small sheet of cardboard. Draw and cut out 6 hexagons of different sizes using the paper cutter. The suggested length of the hexagon sides are 160mm, 80mm, 40mm, 20mm, 10mm and 5mm.
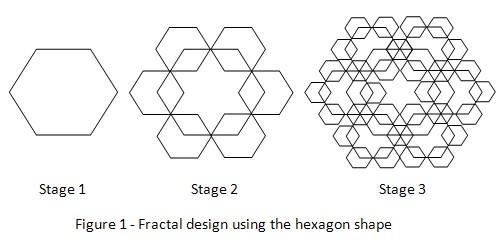
2. Using the hexagon template, draw a160mm hexagon in the center of the paper as shown in figure 1 below. This is the first stage of the fractal image.
3. Proceed to draw the 80mm hexagons on the corners of the hexagon using the template. There will be 6 hexagons drawn as shown in figure 1. This is the completion of the second stage of the image.
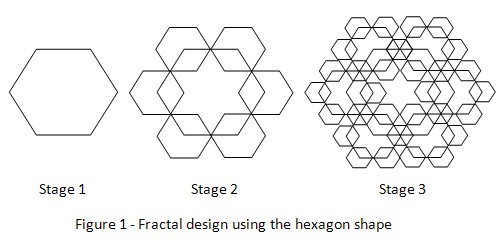
4. Proceed to draw 40mm hexagons around the six corners of the 6 hexagons that were drawn in the second stage. There will be 36 hexagons drawn this time. The third stage of the fractal image is now completed.
5. Proceed to add on the remaining 3 sizes of hexagons using your imagination. An example is given below in figure 2. The positioning of the hexagons can be done selectively to obtain a specific design or shape.
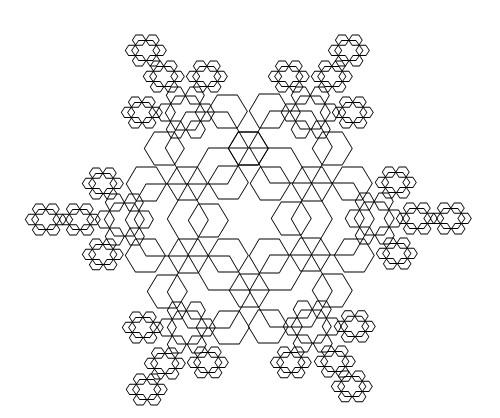
Results
The results show that beautiful designs and creations that were previously unseen and unimaginable, can be created using fractals. The design in Figure 2 below is one such example of fractals using the simple hexagon shape in only 6 stages.
Figure 2 – Example 6th stage fractal design using the hexagon shape
